Polarfuchs (Kolumne): Die Antarktis im Computer – wie funktionieren Computermodelle?
- Article
(846 KB) - Full-text XML
- BibTeX
- EndNote

Es gibt die unterschiedlichsten Methoden, um etwas über den eisigen Kontinent der Antarktis in Erfahrung zu bringen. Manche Forschende ziehen sich ganz warm an und fahren auf Expedition, um vor Ort wichtige Daten, wie Temperaturen, die Eisdicke oder Schneehöhen zu messen. Andere schauen sich die Antarktis aus dem All an: Mit Hilfe von Satelliten messen sie die Veränderungen des großen weißen Eispanzers, dem Eisschild. Durch Satelliten kann man zum Beispiel die Änderung der Dicke messen, die Ausdehnung der Oberflächenschmelze bestimmen oder zählen, wie viele Eisberge vom Eisschild in einer gesetzten Zeit abbrechen. Eine weitere Methode, wie man die Antarktis untersuchen kann, ist sie im Computer “nachzubauen”. Dabei entwickeln Forschende Computermodelle, um verschiedene Prozesse in der Antarktis zu verstehen oder die Zukunft des Eisschildes im Klimawandel zu untersuchen.
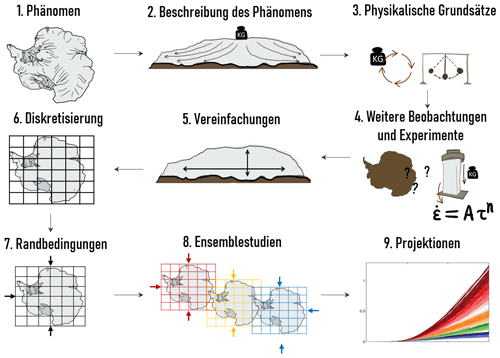
Abb. 1Wie baut man ein Computermodell für die Antarktis? (1) Wir beobachten zum Beispiel, dass sich Gletscher über lange Zeitskalen hinweg bewegen. (2) Wir wissen, dass sich Eis verformt und beginnt aufgrund des eigenen Gewichts zu fließen. (3) Durch physikalische Grundsätze, wie z.B. der Erhalt der Masse und Energie und (4) gezielten Experimenten, erhalten wir die nötigen Gleichungen, die den Eisfluss beschreiben. Für unser Modell brauchen wir zusätzliche Informationen über z.B. die Bodenbeschaffenheit, die einen großen Einfluss auf den Eisfluss hat. (5) Da wir annehmen, dass das Eisschild viel breiter als hoch ist, können wir zum Beispiel bei der Formulierung der Eisgeschwindigkeiten einige Vereinfachungen machen. (6) Wir bringen die mathematischen Gleichungen in eine Form, die der Computer versteht und benutzen ein Gitternetz um für jeden Punkt in der Antarktis die Fließgeschwindigkeit zu berechnen. (7) Wir sagen dem Modell was an den Rändern der Antarktis passiert und (8) indem wir die Randbedingungen oder Modellparameter verändern, können wir eine Vielzahl an Simulationen durchführen. (9) Somit können wir untersuchen wie viel Eis die Antarktis in Zukunft verliert, wenn wir zum Beispiel bestimmte Erwärmungsszenarien (dargestellt durch verschiedene Farben) annehmen. (Übersicht angelehnt an Torsten Albrecht, pers. Mitteilung, 2023.)
Wie man ein Computermodell baut, ist in Abb. 1 dargestellt. Es fängt mit den physikalischen Phänomenen an, die man mit Hilfe des Computers untersuchen will. Zum Beispiel möchte man darstellen, dass sich Eis unter dem großen Gewicht eines Gletschers verformt, bzw. dass das Eis fließt. Dafür braucht man physikalische Gleichungen, die zum Beispiel die Fließgeschwindigkeit beschreiben. Diese werden generell aus physikalischen Grundsätzen wie zum Beispiel der Masse- oder Energieerhaltung hergeleitet. Unbekannte Größen in den Gleichungen können dann eventuell durch Laborexperimenten ermittelt oder angenähert werden. Ein Beispiel für eine Formel, die den Eisfluss beschreibt und auf Experimenten basiert ist „Glen's flaw law“ (siehe Benn and Evans, 2013). Die Formel ist unter Punkt (4) in Abb. 1 zu sehen. Mathematisch sind manche von den ermittelten Gleichungen jedoch etwas kompliziert, sodass man einige Vereinfachungen treffen muss (zum Beispiel mit der sogenannten „Shallow Ice Approximation“; siehe Hutter, 1983). Hat man diese Vereinfachungen gemacht, muss man ein Gitternetz erstellen, in dem jedes Feld einem kleinen Punkt in der Antarktis entspricht. In der Mitte ist meistens der Südpol, oben links die Antarktische Halbinsel und so weiter. Damit das Computermodell für jedes der Felder im Gitternetz die gewünschten Werte ausrechnet, müssen wir die Gleichung noch in eine Form bringen, die der Computer versteht. Diesen Prozess nennt man Diskretisierung. Das heißt, dass man eine kontinuierliche Gleichung in kleinere Stücke aufbrechen muss, damit das Modell hinterher von Gitterpunkt zu Gitterpunkt gehen kann, um die physikalischen Größen wie Eisdicke, Eisgeschwindigkeit oder Temperatur zu berechnen. Nicht nur die Gleichungen müssen diskretisiert werden; in einem Modell muss auch sichergestellt werden, dass es einen stetigen Informationsaustausch zwischen den errechneten physikalischen Größen gibt (auch zum Beispiel zwischen den Gitterpunkten). Dafür müssen viele Zeilen Computercode geschrieben werden. Bevor man einen Modell-Lauf starten kann, muss man dem Modell dann noch sagen, was an den Außenseiten des Gitternetz passiert bzw. was die Randbedingungen des Eises an den jeweiligen Grenzflächen (z.B: zu Ozean oder Atmosphäre) sind: Wie warm ist der Ozean, der an der Unterseite der Eisschelfe, die schwimmenden Fortsätze des Eisschildes, für Schmelzen sorgt? Wie viel schneit es, sodass neues Eis entstehen kann? Das Eismodell kann dann aus allen Informationen und den physikalischen Gleichungen die Eigenschaften des Eises in der Antarktis berechnen.
Wenn alle wichtigen Informationen beisammen sind, kann das Modell mit den Berechnungen beginnen. Je nachdem, was man genau untersuchen möchte, wählt man aus, wie groß ein Feld im Gitternetz sein kann. Manche Forschende wollen sich zum Beispiel nur einen bestimmten Prozess im Modell anschauen, beispielsweise das Abbrechen von Eisbergen vom Eisschild. Dafür brauchen sie andere Einstellungen als diejenigen, die die ferne Zukunft des Eisschildes untersuchen wollen. Für lange Zeitskalen empfiehlt sich eine etwas gröbere Auflösung, weil das Modell für jeden Zeitschritt, in dem es die Antarktis abbilden will, einmal durch alle Zellen oder Gitterfelder durchgehen muss. Je kleiner die Gitterfelder sind, desto länger braucht das Modell deshalb, um die gesamte Antarktis abzubilden. Am Anfang einer Studie braucht es einige Zeit, bis das Modell ein Gleichgewicht erreicht (in dem sogenannten „spin-up“). Das heißt, man lässt das Modell sich einpendeln, sodass es im Gleichgewicht mit den Randbedingungen steht und sich Schneefall, Eisfluss und Schmelze genau in der Waage halten. Danach weiß man: Wie schnell fließt das Eis (in diesem Modell zu den gegebenen Randbedingungen)? Wie dick ist das Eis im Modell oder wo gibt es Eisschelfe? Diese Ergebnisse kann man in einem nachfolgenden Schritt mit gemessenen Eisdicken und Geschwindigkeiten vergleichen.
Ein Computermodell mit dem die Antarktis untersucht werden kann ist zum Beispiel das Parallel Ice Sheet Model, kurz genannt PISM (https://www.pism.io, letzter Zugriff: 3. August 2023; Bueler and Brown, 2009; Winkelmann et al., 2011). Es wird von Forschenden aus Alaska in den USA, sowie aus Potsdam in Deutschland entwickelt. Vor mehr als 10 Jahren wurde damit angefangen, die physikalischen Grundgleichungen in das Modell zu schreiben, sowie die nötigen Bausätze für Teile des Eisschildes einzubauen. Es gibt einen Teil des Modells, der zum Beispiel das Schmelzen an den Unterseiten der großen Eisschelfe berechnet. Ein anderer Teil rechnet aus der vorgegebenen Temperatur (aus den Randbedingungen) aus, wie viel Schmelzen an der Oberseite passiert. In PISM gibt es viele solcher Einzelbauteile, die miteinander Informationen austauschen, damit am Ende ein richtiges Eisschild herauskommt.
Mit einem Computermodell, wie PISM, ist es möglich, wissenschaftliche Experimente durchzuführen. Zum Beispiel wollen Forschende herausfinden, wie viel Eis die Antarktis in den nächsten 100 Jahren verlieren wird, falls die globale Erwärmung nicht gestoppt wird. Diese Art von Experiment kann man unter realen Bedingungen vor Ort natürlich nicht durchführen. Im Modell können aber die ansteigenden Temperaturen in der Atmosphäre und im Ozean als sich verändernde Randbedingungen angenommen werden und somit kann untersucht werden, wie das Eis in der Antarktis reagieren wird. Hierfür werden die Informationen aus globalen oder regionalen Klimamodellen genommen, die einen bestimmten Ausstoß an Treibhausgasen wiederum annehmen (siehe Riahi et al., 2017). Wird nun das Eis-Modell beispielsweise von heute bis zum Jahr 2100 gerechnet, gibt das es aus, wie viel Eis durch die ansteigenden Temperaturen pro Jahr schmilzt oder in das Meer fließen würde (siehe z.B. Winkelmann et al., 2012; Seroussi et al., 2020). Daraus ergibt sich dann eine Kurve, wie stark der Meeresspiegel durch das geschmolzene Eis der Antarktis bis 2100 ansteigt. Modellrechnungen in die Zukunft hinein werden auch “Projektionen” genannt. Dabei ist es nicht wie in der Glaskugel, wo man vielleicht mit Magie die Zukunft vorhersagt: durch die fundierten physikalischen Prozesse, die im Computermodell stecken und die begründete Annahmen, die getroffen werden (wie sich die Temperatur zum Beispiel bis 2100 verändert), kann man eine mögliche Zukunft des Antarktischen Eisschild abbilden. Ganz genau weiß man aber natürlich nicht, wie die Zukunft wird. Um die Unsicherheiten etwas einzugrenzen, werden so genannte “Ensemble” – Studien gemacht, in denen das Modell mit etwas anderen Randbedingungen oder anders gesetzten Stellschrauben (sogenannten Modellparameter) eine Vielzahl an Simulationen rechnet (vgl. Albrecht et al., 2020; Reese et al., 2023). Mit diesen Studien kann man auch die Unsicherheit in den nicht ganz genau bekannten Modellparametern selbst untersuchen. Generell ist es mit einem Computermodell aber möglich, eine wahrscheinliche Zukunft des Eisschildes zu berechnen, die sogenannten Projektionen zu machen – Was man dafür braucht, sind die physikalischen Grundgleichungen, die das Eis beschreiben, das seinen Randbedingungen ausgesetzt ist und ein großer Computer, in dem das Modell konstruiert wird und mit dem die Simulationen gerechnet werden können.
Für diesen Artikel wurden keine Datensätze genutzt.
Die Autorin ist Junior Chief Editor des Journals Polarforschung.
Anmerkung des Verlags: Copernicus Publications bleibt in Bezug auf gerichtliche Ansprüche in veröffentlichten Karten und institutionellen Zugehörigkeiten neutral.
Dank geht an Torsten Albrecht und Elisabeth Stegemann-Nicola, deren wertvolle Kommentare die Qualität des Textes verbesserten und an den/die Gutachter/in für das konstruktive Feedback im Review.
Dieser Artikel wurde von Bernhard Diekmann redaktionell betreut und durch eine:n Expert:in begutachtet.
Albrecht, T., Winkelmann, R., and Levermann, A.: Glacial-cycle simulations of the Antarctic Ice Sheet with the Parallel Ice Sheet Model (PISM) – Part 2: Parameter ensemble analysis, The Cryosphere, 14, 633–656, https://doi.org/10.5194/tc-14-633-2020, 2020. a
Benn, D. and Evans, D. J.: Glaciers and glaciation, Routledge, 2nd Edn., ISBN 978-0-340-90579-1, 2013. a
Bueler, E. and Brown, J.: Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model, J. Geophys. Res.-Earth, 114, F03008, https://doi.org/10.1029/2008JF001179, 2009. a
Hutter, K.: The Application of the Shallow-Ice Approximation, Theoretical Glaciology: Material Science of Ice and the Mechanics of Glaciers and Ice Sheets, 256–332, https://doi.org/10.1007/978-94-015-1167-4_5, 1983. a
Reese, R., Garbe, J., Hill, E. A., Urruty, B., Naughten, K. A., Gagliardini, O., Durand, G., Gillet-Chaulet, F., Gudmundsson, G. H., Chandler, D., Langebroek, P. M., and Winkelmann, R.: The stability of present-day Antarctic grounding lines – Part 2: Onset of irreversible retreat of Amundsen Sea glaciers under current climate on centennial timescales cannot be excluded, The Cryosphere, 17, 3761–3783, https://doi.org/10.5194/tc-17-3761-2023, 2023. a
Riahi, K., Van Vuuren, D. P., Kriegler, E., Edmonds, J., O’Neill, B. C., Fujimori, S., Bauer, N., Calvin, K., Dellink, R., Fricko, O., Lutz, W., Popp, A., Crespo Cuaresma, J., KC, S., Leimbach, M., Jiang, L., Kram, T., Rao, S., Emmerling, J., Ebi, K., Hasegawa, T., Havlik, P., Humpenöder, F., Da Silva, L. A., Smith, S., Stehfest, E., Bosetti, V., Eom, J., Gernaat, D., Masui, T., Rogelj, J., Strefler, J., Drouet, L., Krey, V., Luderer, G., Harmsen, M., Takahashi, M., Baumstark, L., Doelman, J. C., Kainuma, M., Klimont, Z., Marangoni, G., Lotze-Campen, H., Obersteiner, M., Tabeau, A., and Tavon, M.: The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview, Global Environ. Chang., 42, 153–168, https://doi.org/10.1016/j.gloenvcha.2016.05.009, 2017. a
Seroussi, H., Nowicki, S., Payne, A. J., Goelzer, H., Lipscomb, W. H., Abe-Ouchi, A., Agosta, C., Albrecht, T., Asay-Davis, X., Barthel, A., Calov, R., Cullather, R., Dumas, C., Galton-Fenzi, B. K., Gladstone, R., Golledge, N. R., Gregory, J. M., Greve, R., Hattermann, T., Hoffman, M. J., Humbert, A., Huybrechts, P., Jourdain, N. C., Kleiner, T., Larour, E., Leguy, G. R., Lowry, D. P., Little, C. M., Morlighem, M., Pattyn, F., Pelle, T., Price, S. F., Quiquet, A., Reese, R., Schlegel, N.-J., Shepherd, A., Simon, E., Smith, R. S., Straneo, F., Sun, S., Trusel, L. D., Van Breedam, J., van de Wal, R. S. W., Winkelmann, R., Zhao, C., Zhang, T., and Zwinger, T.: ISMIP6 Antarctica: a multi-model ensemble of the Antarctic ice sheet evolution over the 21st century, The Cryosphere, 14, 3033–3070, https://doi.org/10.5194/tc-14-3033-2020, 2020. a
Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 1: Model description, The Cryosphere, 5, 715–726, https://doi.org/10.5194/tc-5-715-2011, 2011. a
Winkelmann, R., Levermann, A., Martin, M. A., and Frieler, K.: Increased future ice discharge from Antarctica owing to higher snowfall, Nature, 492, 239–242, 2012. a





